溶媒抽出法の計算

今回の問題

今回は平成29年度第1種放射線取扱主任者試験「化学」より溶媒抽出法についての問題を解説していきます。

なお、問題文は原子力安全技術センターHPより引用しております。

問題20

ある化学種に対する有機溶媒（O）と水（W）の間の分配比（O/W）は４ある。その化学種（100MBq）を含む水溶液に同体積の有機溶媒を加えて抽出した。有機溶媒を取り除き、残った水溶液に同体積の新たな有機溶媒を加えて再び抽出した。２回の操作で有機溶媒に抽出された化学種の放射能の総量［MBq］として、最も近い値は次のうちどれか。

1. 4

2. 20

3. 80

4. 90

5. 96

解説

溶媒抽出法における基本公式

溶媒抽出法における重要な式は以下の通りになります

問題文の理解

はじめに問題文を簡略化する作業に入りましょう

1. 水溶液（D=4の化学種100MBqを含む：以下省略）を同体積の有機溶媒を加えて抽出した
2. 残った水溶液に対して再度同体積の有機溶媒を加えて抽出した
3. 有機溶媒へ抽出された総放射能は？

イメージ図は下図参照↓↓↓

図からもわかるように求める解の有機溶媒に抽出された総放射能とは「③a と ③b の和」である

【※】以下、図を参照に各溶媒抽出を①、②と区分けする（例：水溶液①など）

解法

抽出後の有機溶媒中の各放射能③a及び③bを求め、求めるべき解である有機溶媒中の総放射能（③a+③b）を求める流れで説明します

③a を求める

基本公式より（問題文から分配比D=4、同体積のより\( \frac{V_o}{V_w} =1\) ）

$$E=\frac{４}{４+１}=\frac{4}{5}$$

③a の放射能は抽出率と水溶液①の放射能の積で求まるので

$$③a = \frac{4}{5}*100=80\qquad[MBq]$$

③a の放射能は80MBqである

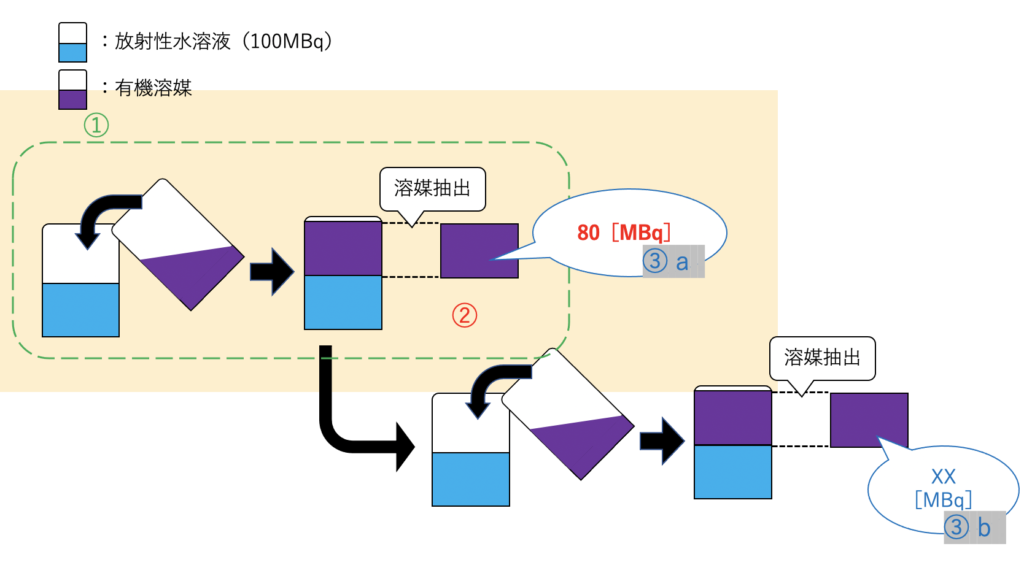
③b を求める

抽出率については③aを求めた時と同条件（問題文から分配比D=4、同体積のより\( \frac{V_o}{V_w} =1\) ）のため抽出率は同じである

③b の放射能は抽出率と水溶液②の放射能の積で求まるが、「この時の水溶液②は溶媒抽出後に再度分離し使用した水溶液である」為、初期値から分離した③a分の放射能を引かなければならない。

$$水溶液②＝100-80=20\qquad[MBq]$$

水溶液②の放射能は20MBqである。

③b の放射能は抽出率と水溶液②の放射能の積より

$$③a = \frac{4}{5}*20=16\qquad[MBq]$$

③b の放射能は16MBqである

お疲れ様でした。