問題
今回は第71回診療放射線国家試験「放射線治療学」より標準測定法12に基づく光子の水吸収線量評価についての問題を解説していきます。
なお、問題文は厚生労働省HPより引用しております。
午後36
標準測定法12に基づく光子線の電離箱線量計を用いた基準条件における水吸収線量評価について正しいのはどれか。ただし、温度・気圧は標準条件とする。
1. SSDが長くなると、過大評価となる
2. 気圧を高く読み間違えると、過大評価となる
3. 温度を高く読み間違えると、過大評価となる
4. 電離箱を深い位置に誤設置した場合、過大評価となる
5. ファーマ形電離箱の実効中心をアイソセンタに誤設置した場合、過大評価となる
解説
水吸収線量評価における重要知識
光子の水吸収線量
$$D[Gy]=\frac{E[J]}{m[kg]}$$
をもとに本問題に関する要点2つをまとめます
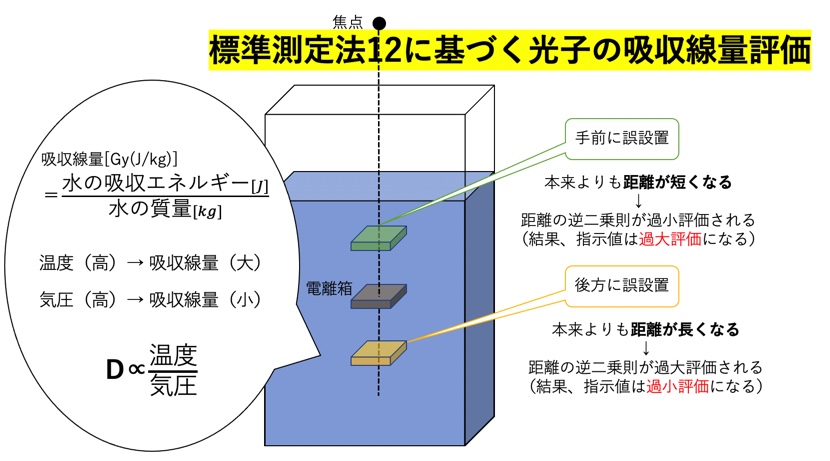
(1)温度・気圧と吸収線量の関係
温度・気圧に対する補正は水吸収線量における水の質量に対するものであります
まず始めに密度と温度・気圧の関係を以下の表に表します
| 高くなる(上がる) | 低くなる(下がる) | |
| 温度 | 低密度 | 高密度 |
| 気圧 | 高密度 | 低密度 |
これは丸暗記するものではありません。
身近な例を用いて理解してください。例えば、気球が浮いているのを想像して下さい。空気を熱する(温度を上げる)と膨張より風船内の空気は周囲の空気の密度よりも低くなることで浮力が生じます。また、空気に圧力をかけてあげると密度が高くなることは想像できます。密度と質量は比例関係であるので
- 温度(高):軽い
- 気圧(高):重い
となります。ですが吸収線量での質量は分母に存在するので温度・気圧の影響は吸収線量としては反比例になります
- 温度(高):軽い → 吸収線量:大きくなる
- 気圧(高):重い → 吸収線量:小さくなる

ちなみに温度・気圧を補正する補正式として\(K_{TP}\)がありますが、頑張って覚えなければならない式ではありません(ですが、標準気温は22℃は覚えたほうがいいでしょう)
$$K_{TP}=\frac{273.2+t}{273.2+22}・\frac{1013.3}{P}$$
(2)距離と水吸収エネルギー減弱の関係
距離の逆二乗則に従って線量が減少するのは有名な放射線の現象であります
線量とありますが放射線の数が逆二乗則に従って減少するということはその放射線が水に与えるはずのエネルギーも減少していく事は容易に想像できます。

<距離の逆二乗則の過大・過小評価について>
距離の逆二乗則とは距離の応じて同面積を貫く放射線量が”距離の逆二乗分”だけ減少することを表したものである(上図左側参照)
ここで電離箱を前方へ誤設置した例をとると、距離の逆二乗則が過小評価される事になる。それは電離箱へ到達する放射線量が本来量よりも増加するという事である。従って、放射線量が増加された状態で計算されるので吸収線量もその分増加(過大評価)する事になる。これは逆も同様である
解法
それでは今までの知識をもとに選択肢を解いていきましょう
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
1. SSDが長くなると、過大評価となる
SSDが長いとは距離が長いと同じであるため、
距離(長)→ 距離の逆二乗則(過大評価)→ 吸収線量(過小評価)
よってSSDが長いと過小評価なので「不正解」
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
2. 気圧を高く読み間違えると、過大評価となる
気圧(高)→ 密度(高)→ 質量(大)(→ 吸収線量の分母(大))→吸収線量(小)
よって気圧が高いと過小評価なので「不正解」
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
3. 温度を高く読み間違えると、過大評価となる
温度(高)→ 密度(低)→ 質量(小)(→吸収線量の分母(小))→ 吸収線量(大)
よって温度が高いと過大評価であるのでこれは「正解」
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
4. 電離箱を深い位置に誤設置した場合、過大評価となる
深い位置の誤設置は距離が長くなるのと同等であるため
距離(長)→ 距離の逆二乗則(過大評価)→ 吸収線量(過小評価)
よって深い誤設置は過小評価なので「不正解」
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
5. ファーマ形電離箱の実効中心をアイソセンタに誤設置した場合、過大評価となる
標準測定法12での吸収線量測定ではファーマ形電離箱は幾何学中心で測定する。(実効中心は幾何学中心よりも前方(0.6cyl)に位置する)
本来幾何学中心をアイソセンタに設置するはずが、誤って実効中心で設置する事によって幾何学中心は実効中心分だけ後方に、すなわち深い位置に誤設置されたという事になります。

距離(深)→ 距離の逆二乗則(過大評価)→ 吸収線量(過小評価)
よって深い誤設置は過小評価なので「不正解」
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
従って、正しい選択肢は【3】である
お疲れ様でした
コメント