問題
今回は第71回診療放射線国家試験「医用工学」より交流回路の周波数特性についての問題を解説していきます。
なお、問題文は厚生労働省HPより引用しております。
午後75
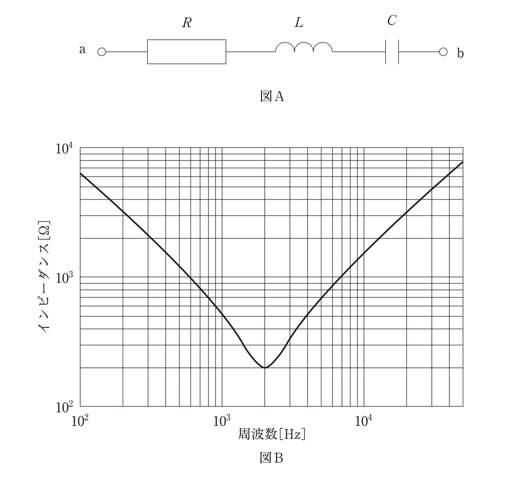
図Aの回路のa-b間に正弦波交流電圧を加えた時の合成インピーダンスの周波数特性を図Bに示す。抵抗R[kΩ]、誘導リアクタンス[mH]及び静電容量C[μF]に最も近い値の組合せはどれか。
R ー L ー C
1. 0.2 ー 0.25 ー 25
2. 0.2 ー 25 ー 0.25
3. 0.25 ー 0.2 ー 25
4. 0.25 ー 25 ー 0.2
5. 25 ー 0.25 ー 0.2
解説
今回はQ値を使わずに簡単に求められる方法を解説していきます。
交流回路の基本式
合成インピーダンス:Z
$$Z=\sqrt{R^2+(X_L-X_C)^2}$$
上式より合成インピーダンスZが最小のときZ=Rである
リアクタンスと周波数の関係
周波数を f とする
●誘導性リアクタンス:\(X_L\)
$$X_L=2πfL$$
上式より、\(X_L∝周波数[f]\):比例関係にある
【高周波領域では誘導性支配:\(Z≒X_L\)】
●容量性リアクタンス:\(X_C\)
$$X_C=\frac{1}{\sqrt{2πfC}}$$
上式より、\(X_C∝\frac{1}{周波数[f]}\):反比例関係にある
【低周波領域では誘導性支配:\(Z≒X_C\)】
解法
▷抵抗(\(R\))を求める
抵抗値は合成インピーダンスの式より周波数が最も小さい値を選択すれば良い

上図より抵抗(\(R\))は0.2kΩである
▷誘導性リアクタンス(\(X_L\))を求める
(リアクタンスと周波数の関係より)誘導性リアクタンスは高周波領域で誘導性支配となる
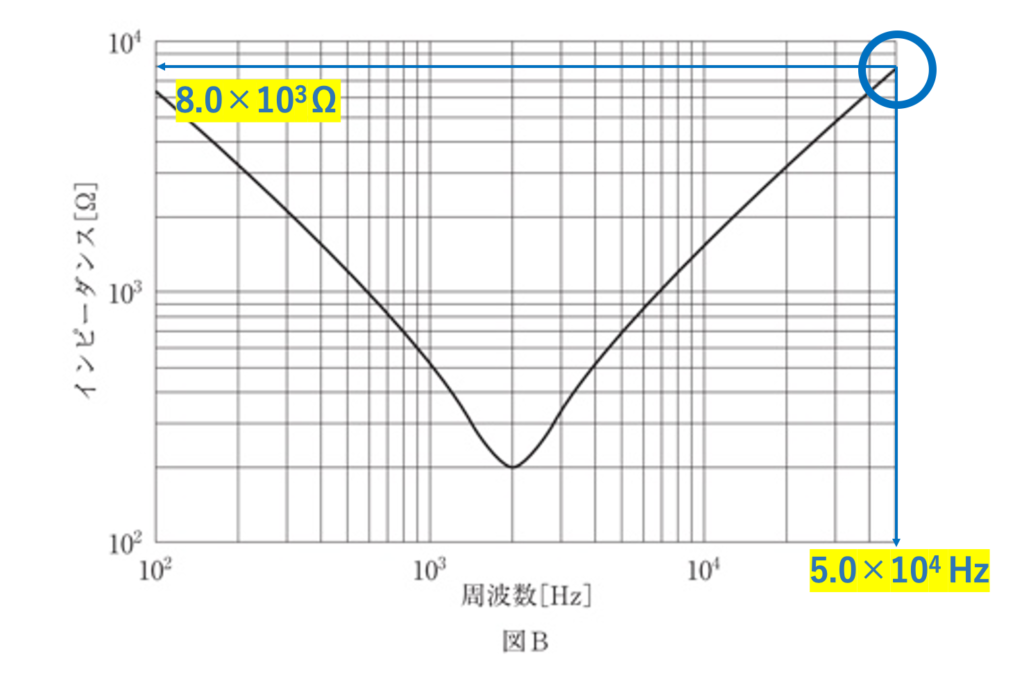
最大周波数50kHzでのインピーダンスは約8000Ωであり、抵抗及び容量性リアクタンスが合成インピーダンスに占める割合はかなり低いので\(Z≒X_L\)で近似する(誘導支配)
$$Z≒X_L=2πfL$$
周波数50kHzでインピーダンスは8000Ω(8kΩ)を代入すると
$$8k=2π・50k・L$$
$$L=\frac{8k}{2π・50k}≒0.025$$
従って、\(L=25mH\)である
▷容量性リアクタンス(\(X_C\))を求める
(リアクタンスと周波数の関係より)容量性リアクタンスは低周波領域で容量性支配となる

最小周波数100kHzでのインピーダンスは約6500Ωであり、抵抗及び誘導性リアクタンスが合成インピーダンスに占める割合はかなり低いので\(Z≒X_C\)で近似する(容量支配)
$$Z≒X_C=\frac{1}{\sqrt{2πfC}}$$
周波数100kHzではインピーダンスは約6500Ω(6.5kΩ)を代入すると
$$6.5k=\frac{1}{\sqrt{2π・100・C }}$$
$$C=\frac{1}{\sqrt{2π・100・6.5k}}≒0.25×10^{-6}$$
従って、\(C=0.25μF\)である
以上をまとめると
- R=0.2Ω
- L=25mH
- C=0.25μF
より選択肢は【2】になります。
お疲れ様でした

コメント