今回の問題
今回は第62回診療放射線国家試験「放射線安全管理学」より放射能の線源交換日についての問題を解説していきます。
なお、問題文は厚生労働省HPより引用しております。
問102
\(^{192}Ir\)線源の放射能が1/3に減衰したときに線源交換を行うとした。交換日に最も近い日数はどれか。ただし、\(^{192}Ir\)の半減期を74日とし、\(\log_{e}{2}=0.693\)、\(\log_{e}{3}=1.099\)とする。
1. 100
2. 110
3. 120
4. 130
5. 140
解説
問題の理解
これは放射能の減衰について問われている問題です。
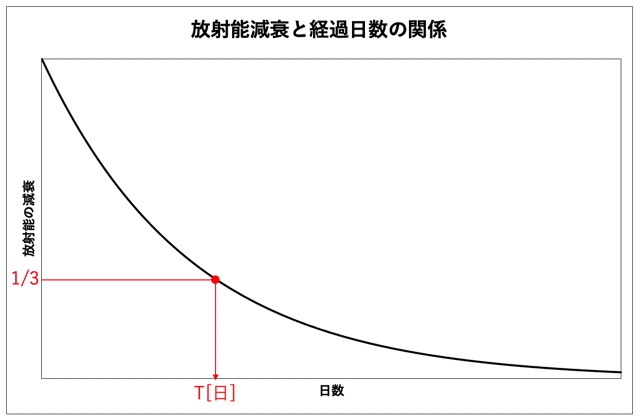
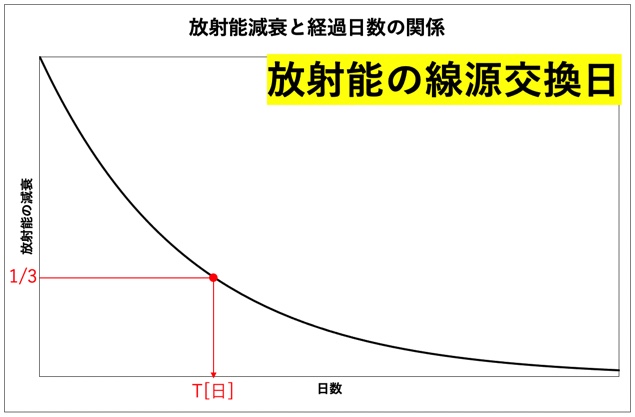
見覚えのあるグラフですね。そうです、半減期を学習する際に見るグラフです。
ですが半減期の式を単に暗記している場合はこの問題を解くのが困難になりますので導出できるようにしましょう
放射能減衰の基本式
放射能が 1/N に減衰する日数をT(N)とした以下の関係になります。\(T_{1/2}\)は半減期とする
$$T(N)=\frac{\log_{e}{N}}{0.693}×T_{1/2}$$
ですが、これは覚えなくてもいい式なので自分で導出できるようにしましょう
<導出>
放射能の式\(A=A_o・e^{-λt}\)より放射能が1/Nになる時を考える。このときに経過している日数をT(N)とする
放射能が1/Nになるというのは、「初期値に対して放射能が1/Nになる」ということなので放射能の式を整理すると
$$\frac{A}{A_o}=\frac{1}{N}=e^{-λ・T(N)}$$
両辺\(\log_{e}\)でとると
$$\log_{e}{N}=λ・T(N)$$
ここで\(λ=\frac{0.693}{T_{1/2}}\)より式を整理すると
$$T(N)=\frac{\log_{e}{N}}{0.693}×T_{1/2}$$
解法
放射能減衰の基本式を使って求めていきます。(何度も言いますが導出できるように理解しましょう)
問題文より
- 1/N → 1/3
- 半減期\(T_{1/2}\):74日
- \(log_{e}{3}\)=1.099
式\(\hspace{5pt}T(N)=\frac{\log_{e}{N}}{0.693}×T_{1/2}\)に代入すると
$$T(N)=\frac{1.099}{0.693}×74≒117$$
よって線源交換日は117日であり、最も近い選択肢は120日の【3】になります
お疲れ様でした

コメント