今回は令和3年度第1種放射線取扱主任者試験「実務」より誤差の伝播式についての問題を解説していきます。
なお、問題文は原子力安全技術センターHPより引用しております。
問1(II)【イ】
解法
(イ)機器効率の誤差を求める
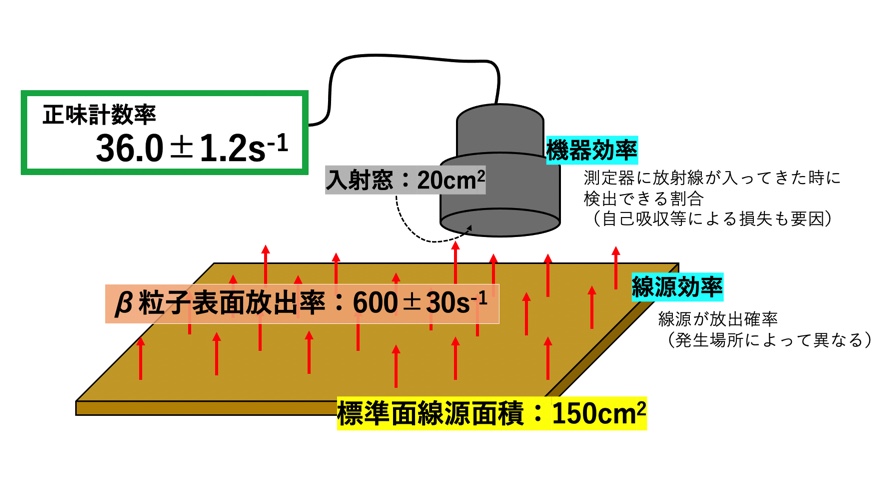
問題文より計算式に必要な情報を抜き出してみましょう
- β粒子表面放出率:\(600±30s^{-1}\)
- 正味の計数率:\(36.0±1.2s^{-1}\)
- 標準面線源面積:\(150cm^2\)
- 入射窓面積:\(20cm^2\)
機器効率\(ε_i\)の式は
$$ε_i=\frac{n}{E_{SC}・W}$$
- n:正味の計数率
- \(E_{SC}\):単位標準面線源面積当たりのβ粒子表面放出率
- W:入射窓面積
。。。ですが、機器効率とは「放出された放射線をどのくらいの割合で検知されるか」の度合いであるので考えながら求めていきましょう
※個人的にはあまり覚えるべき公式とは思っていません
- ⑴標準面線源の単位面積当たりのβ線の放出率を求める
- ⑵①で求めた値を入射窓(測定面積)倍すれば検出器に対応するβ線放出率がわかる
- ⑶②で求めた値を機器効率倍すれば測定器の正味計数率が求まる
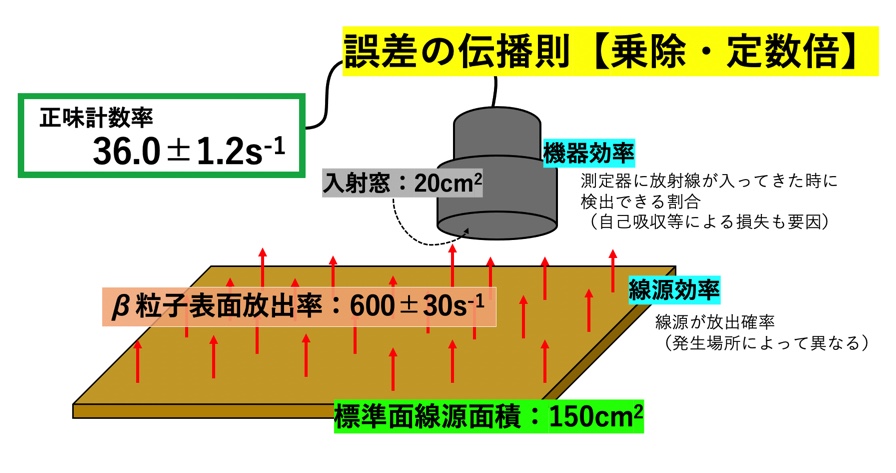
この計算過程で標準偏差(誤差)を持つ数値同士の計算を行う為、「誤差の伝播則」という公式を使いましょう
誤差の伝播則(乗除・定数倍)
・定数倍
$$a×(x±y)=ax±ay$$
・乗算
$$(a±b)×(x±y)=ax±ax\sqrt{\left(\frac{b}{a}\right)^2+\left(\frac{y}{x}\right)^2}$$
・除算
$$(a±b)÷(x±y)=\frac{a}{x}±\frac{a}{x}\sqrt{\left(\frac{b}{a}\right)^2+\left(\frac{y}{x}\right)^2}$$
※乗算、除算は(誤差小さい時は)その誤差の扱いは同じである
STEP1:標準面線源の単位面積当たりのβ線の放出率を求める
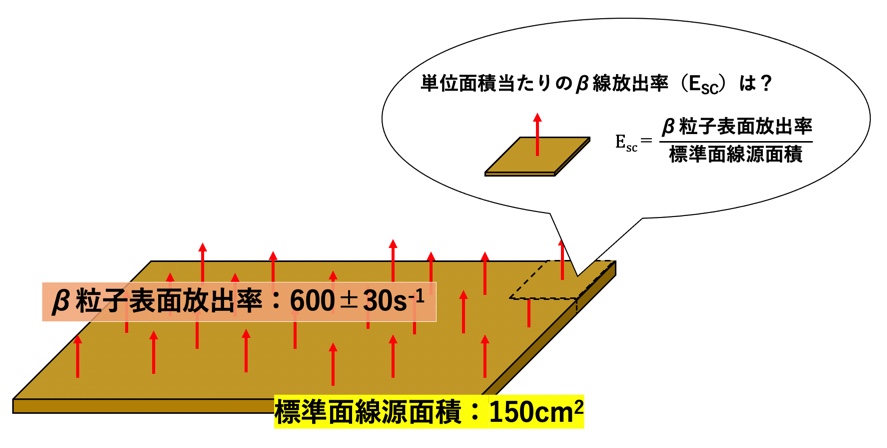
単位面積あたりのβ線放出率\(E_{SC}\)は、
$$E_{SC}=\frac{600±30}{150}$$
ここで、誤差の伝播則「定数倍」を使うと
$$E_{SC}=\frac{1}{150}・(600±30)=\frac{600}{150}±\frac{30}{150}$$
と置き換えられこれを計算すると、\(40.0±0.2\)になる
STEP2:STEP1で求めた値を入射窓(測定面積)倍すれば検出器に対応するβ線放出率がわかる
これもSTEP1と同様に計算を行うと
$$E_{SC}・W=20・(40±0.2)=80±4$$
よって、入射窓に入ってくるβ線の放出率は\(80.0±4.0\)である
STEP3:STEP2で求めた値を機器効率倍すれば測定器の正味計数率が求まる
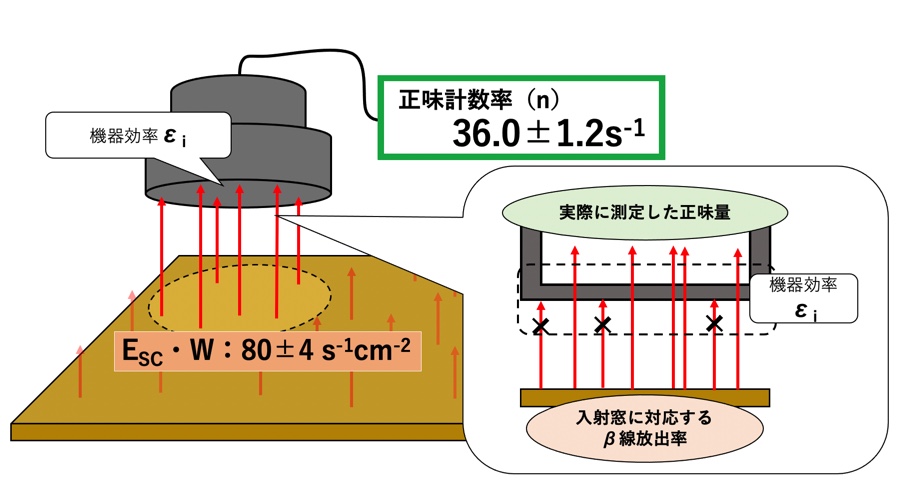
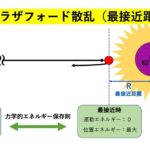
上図(右側)を式で表したら、
入射窓に対応するβ線放出率×機器効率=正味計数率
となる。今回は機器効率を求める為、上式を変形して計算すると
$$ε_i=\frac{36±1.2}{80±4}$$
となる。ここで誤差の伝播則「除算」を用いて計算すれば
$$ε_i=\frac{36}{80}±\frac{36}{80}\sqrt{\left(\frac{1.2}{36}\right)^2+\left(\frac{4}{80}\right)^2}$$
$$≒0.45±0.45\sqrt{(0.033)^2+(0.05)^2}$$
$$=0.45±0.45\sqrt{0.0035}$$
$$=0.45±0.45・\frac{1}{100}\sqrt{35}$$
\(6^2=36\)で近似すれば
$$=0.45±0.45・\frac{6}{100}=0.45±0.027$$
今回は選択肢に0.03があるのでそちらが正解となります。
お疲れ様でした

コメント