問題
今回は令和3年度第1種放射線取扱主任者試験「物理学」よりα線のラザフォード散乱についての問題を解説していきます。
なお、問題文は原子力安全技術センターHPより引用しております。
問17
真空中で鉛の原子核(原子番号82)に5.0MeVのα粒子が向かうとき、α粒子がクーロン力に逆らって鉛の原子核に最接近する距離[fm]として最も近い値は次のうちどれか。ここで、真空中の誘電率を\(8.9×10^{-12}・C^2・N^{-1}・m^{-2}\)とする。
1. 12
2. 24
3. 48
4. 96
5. 192
解法
問題の理解
今回の問題が求めていることについて図を使ってまとめてみましょう
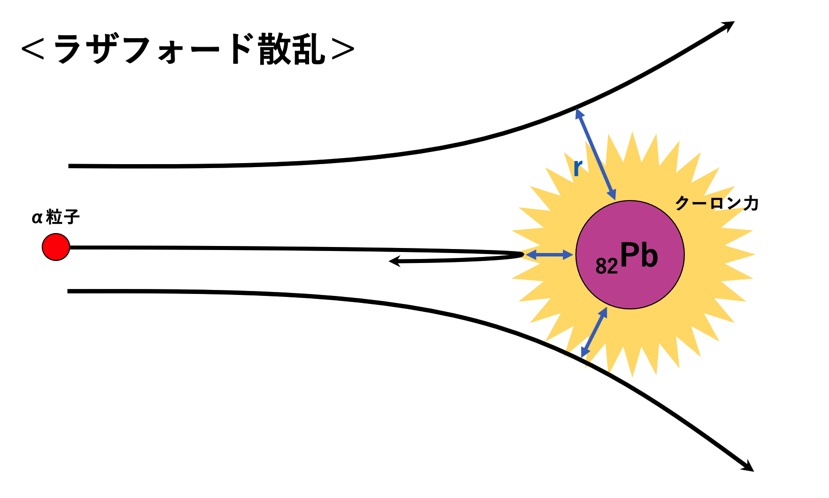
α粒子は鉛原子核に入射する際、鉛原子核の持つクーロン力によってその軌道は変化する(散乱)。今回の問題はα粒子と鉛原子核が最も近づく距離(最接近距離)を求めれば良い
α粒子と鉛原子核の最接近距離を考えるとき、クーロン力を考慮すればα粒子は鉛原子核の延長上より、すなわちd=0で入射すれば良いことがわかる。この時クーロン力によって散乱する角度をθとすれば、d=0でθ=180°となる(下図参照)

α粒子の最接近距離
ようやくα粒子と鉛原子核の最接近距離について計算してみる
ここでα粒子の力学的エネルギーについて考えると
(無限遠方でのエネルギー和)=(最接近時のエネルギー和)
となる。ここでいう無限遠方とは鉛原子核によるクーロン力を無視できる距離、すなわち(電気的)位置エネルギーが0の地点とする
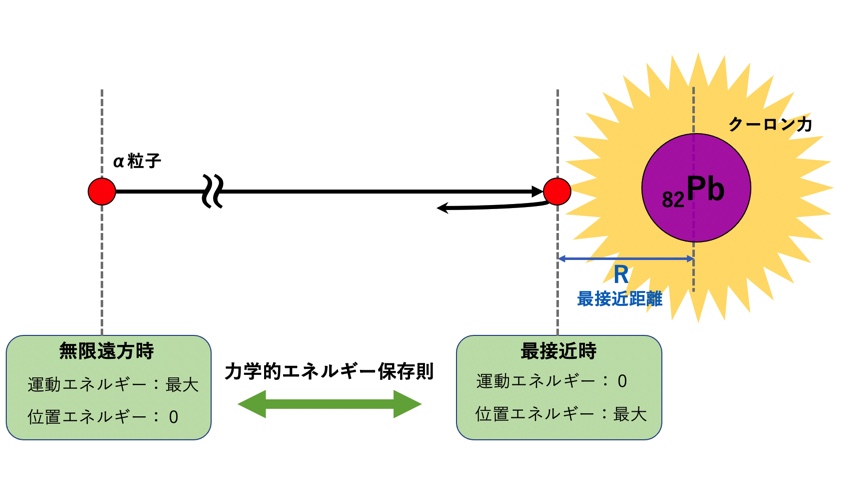
(無限遠方でのエネルギー和)=(最接近時のエネルギー和)
力学的エネルギー保存則を利用して式を考えてみよう
- 無限遠方時の運動エネルギー:問題文よりE=5.0MeV
- 無限遠方時の位置エネルギー:0
- 最接近時の運動エネルギー :0
- 最接近時の位置エネルギー :最接近距離Rでの電気的位置エネルギー
となり
$$E+0=0+\frac{k・Q_1・Q_2}{R}・・・(A)$$
となる。ここで、電気的位置エネルギーUは比例定数k(\(9.0×10^9\))を用いて
$$U=\frac{k・Q_1・Q_2}{R}$$
で表す
(A)式を最接近距離Rの式で変形すると
$$R=\frac{k・Q_1・Q_2}{E}・・・(1)$$
となり、これを求めれば良い
各々の文字式
- E:α粒子の運動エネルギー(5MeV)
- \(Q_1\):α粒子の電荷(2e)
- \(Q_2\):鉛原子核の電荷(82e)
これを(1)式に代入すると
$$R=\frac{9×10^9・2e・82e}{5MeV}$$
素電荷\(e[C]=1.6×10^{-19}\)、またエネルギー単位換算\(1[eV]=1.6×10^{-19}[J]\)でまとめると
$$R=\frac{(9×10^9)×2×82×(1.6×10^{-19})^2}{(5×10^6)×1.6×10^{-19}}$$
これを計算すると
$$R=472.32×10^{-16}$$
求める距離は[fm]である為(\(f=10^{-15}\))
R≒47fmとなり選択肢は【3】になります
お疲れ様でした
コメント