問題
今回は第70回診療放射線国家試験「医用工学」より医療統計の計算例についての問題を解説していきます。
なお、問題文は厚生労働省HPより引用しております。
午前94
ある癌診断の画像検査で、真陽性率が98%、偽陽性率が5%であった。この癌の一般的な罹患率は1%である。ある人がこの画像検査を受けて陽性と判断されたとき、実際に癌に罹患している確率に最も近いのはどれか。
1. 10%
2. 17%
3. 25%
4. 67%
5. 95%
解法
罹患者数と陽性者数の違い
例えば下図のような状態を考える。罹患率10%の癌に対して真陽性率80%、偽陽性率10%
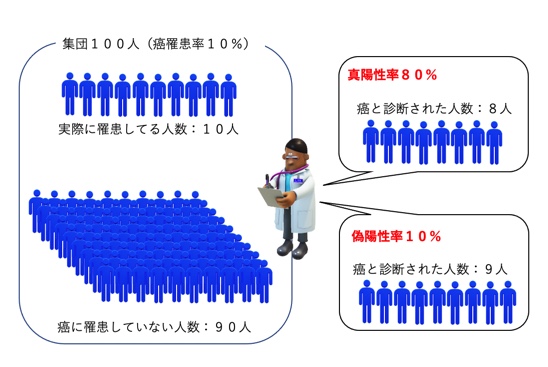
ここで罹患者数は10人(集団100人中)、真陽性者数は8人である。これはどういう計算をしたのでしょうか。
真陽性者数=(対象数 × 罹患率)× 真陽性率=(100 × 0.1)× 0.8=8
同様に偽陽性者数は
偽陽性者数=(対象数 × (1ー罹患率))× 偽陽性率 =100 ×(1 – 0.1)× 0.1 = 9
となる。ここで陽性と判断されたときに実際に罹患している確率をPとすると
$$P=\frac{真陽性者数}{真陽性者数+偽陽性者数}$$
となる。ここでPは真陽性者数と偽陽性者数で構成される式のため対象数が仮に未知でも約分することによって求めることができる。すなわち、Pを求めるために対象者の項目は消去できる。
解説
それでは問題に戻ります
ある癌診断の画像検査で、真陽性率が98%、偽陽性率が5%であった。この癌の一般的な罹患率は1%である。ある人がこの画像検査を受けて陽性と判断されたとき、実際に癌に罹患している確率に最も近いのはどれか。
求める問いは「陽性と判断されて本当に罹患している確率」になりこれをPとおきます。
まずは目標とする式を考えましょう
$$P=\frac{本当に罹患している患者数}{陽性と判断された患者数}=\frac{真陽性者数}{真陽性者数+偽陽性者数}$$
次にその式に対応する各項目について考えましょう
真陽性者数=(対象数 × 罹患率)× 真陽性率
偽陽性者数=(対象数 × (1ー罹患率))× 偽陽性率
ここで対象者数は未知なのでそのまま消去して、問題文よりまとめると(便利上有効数字は無視する)
$$真陽性者数=0.01× 0.98 =9.8×10^{-3}$$
$$偽陽性者数=(1- 0.01)× 0.05=49.5×10^{-3}$$
よってPを求めると
$$P=\frac{9.8×10^{-3}}{(9.8×10^{-3})+(49.5×10^{-3})}=\frac{9.8}{9.8+49.5}$$
P=0.1652….となるため選択肢の最も近い17%【2】が正解となる
お疲れ様でした



コメント