分岐壊変の応用問題

問題

今回は令和元年度第1種放射線取扱主任者試験「化学」より分岐壊変についての問題を解説していきます。

なお、問題文は原子力安全技術センターHPより引用しております。

問８

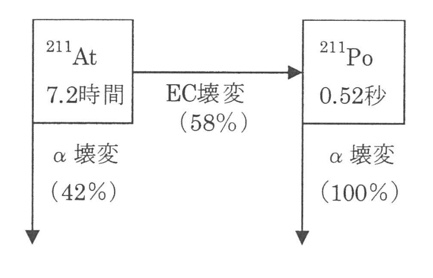
\(^{211}At\)は、42％がα壊変して\(^{207}Bi\)に、58％はEC壊変して\(^{211}Po\)になる。\(^{211}Po\)はα壊変する。\(^{211}At\)と\(^{211}Po\)の半減期はそれぞれ7.2時間と0.52秒である。\(^{211}At\)と\(^{211}Po\)が放射平衡にあるとき、\(^{211}At\)と\(^{211}Po\)が単位時間に放出するα線の数をそれぞれ\(N_{At}\)と\(N_{Po}\)とすると、これらの比（\(N_{At}/N_{Po}\)）として最も近い値は、次のうちどれか。

1. 0.3

2. 0.7

3. 1.4

4. 2.4

5. 3.6

解法

分岐壊変とは

放射性核種の崩壊において親核が複数の崩壊形式をとる時、それらの崩壊をまとめて分岐壊変という

• 単に崩壊・・・α壊変、β壊変、など
• 分岐壊変・・・α壊変とEC壊変、β壊変とγ崩壊、などの複数崩壊

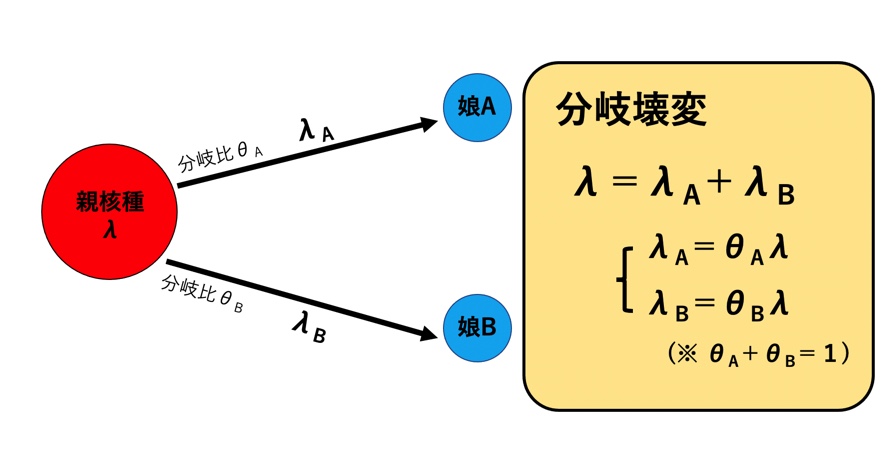
ここで親核X（壊変定数：λ）と分岐壊変で生成される娘核\(Y_{A}\)、\(Y_{B}\)（壊変定数：\(λ_{A}\)、\(λ_{B}\)）とする時の壊変定数の関係は

$$λ=λ_A+λ_B$$

が成り立つ。さらにそれぞれの分岐壊変の割合（分岐比）を\(θ_{A}\)、\(θ_{B}\)とすると

$$λ_A=θ_A・λ$$

$$λ_B=θ_B・λ$$

となる

解説

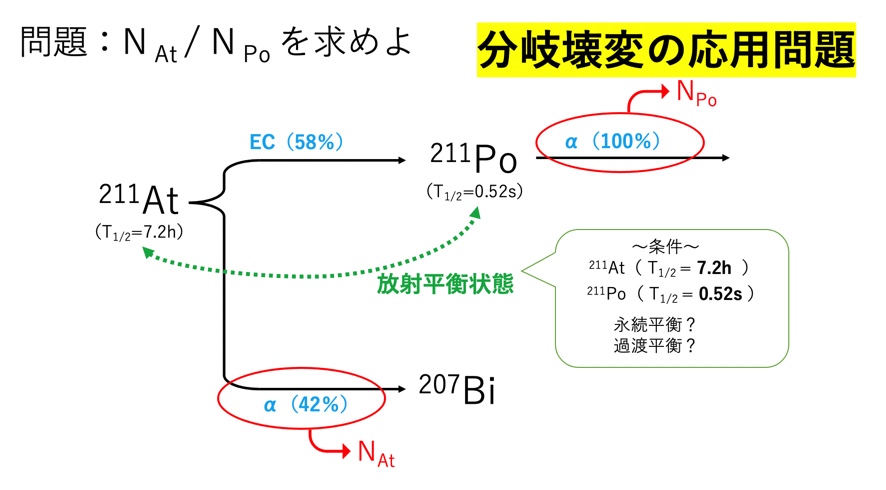
それでは本題に戻りましょう。問題を元に改めて図を作ってみると下のようになります

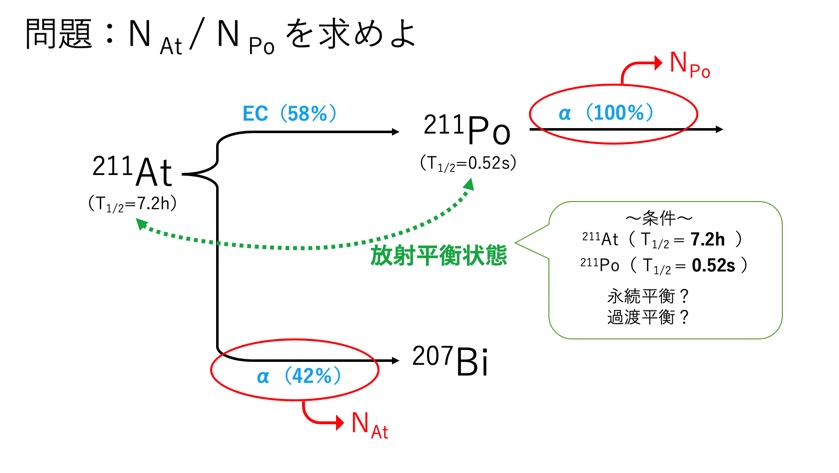
上図より求めるべきポイントを押さえます

STEP⑴：\(^{211}At\)より分岐壊変する割合よりα崩壊における放射能を求める（\(N_{At}\)）

放射能の式\(A=λN\)より\(λ\)の分岐壊変について考える

$$A_{α}=λ_{α}・N$$

ここで\(λ_{α}\)は\(^{211}At\)の崩壊定数\(λ\)に対して分岐比42％で分岐壊変することから

$$λ_{α}=0.42・λ$$

$$A_{α}=0.42λ・N$$

となる

STEP⑵：\(^{211}At\)と\(^{211}Po\)が放射平衡である事を元に\(^{211}Po\)の放射能を求める（\(N_{Po}\)）

\(^{211}At\)と\(^{211}Po\)はそれぞれ半減期が7.2時間、0.52秒でありこのような極端に娘核種の半減期が短い場合での放射平衡は「永続平衡」が成立する

永続平衡では（親核種の放射能）＝（娘核種の放射能）となる為、\(^{211}At\)のEC壊変における放射能は\(^{211}Po\)の放射能と等しくなる

※また\(^{211}Po\)は100％でα壊変する為、分岐比は１となる

（\(N_{Po}\)）＝（\(^{211}At\)のEC壊変における放射能）と置き換えることができるから\(^{211}At\)のEC壊変における放射能は分岐比58％のためSTEP⑴と同様に計算すると

$$N_{Po}=A_{EC}=0.58λN$$

となる。

以上のことより求めるべき（\(N_{At}/N_{Po}\)）は

$$\frac{N_{At}}{N_{Po}}=\frac{0.42λN}{0.58λN}=0.7241…$$

従って答えは0.72となり最も近い選択肢は【２】になります

お疲れ様でした