SUVの計算

問題

今回は「核医学検査技術学」よりSUVの計算についての問題を解説していきます。

核医学分野において計算問題としては頻出である為ここでしっかりと理解しましょう

問題

9時00分に300MBqあった\( ^{18}F-FDG\)を11時40分に患者へ全量投与した。12時40分に撮影を開始し、13時30分に定量解析を行ったところ病変部の放射能濃度は7.5kBq/mLであった。病変部のSUVはどれか。但し、患者の年齢は75歳、身長170cm、体重60kgとし、\( ^{18}F-FDG\)の半減期を110分、人体の密度を1kg/Lとする

1. 1.5

2. 3.0

3. 4.5

4. 6.0

5. 7.5

解法

SUVの定義

SUVとはPET検査において病変へPET薬剤の集積度合について画像より計測される定量値であります

$$SUV=\frac{目的組織の放射能濃度}{人体の放射能濃度}=\frac{目的組織の放射能濃度}{\frac{投与放射能量}{体重}}$$

で求まります。

理想論では均等に集積すればSUV=1になります

ですが実際は生理的に集積する部位、特異的に薬剤を取り込む部位（腫瘍等）が存在します

ここで絶対に押さえておくべきポイントは

「SUVの計算では投与した放射能の時間経過をしっかりと把握することが大切」

であることです。逆にこれさえ押さえていればSUVの計算はとても簡単に感じます。

SUVの導出

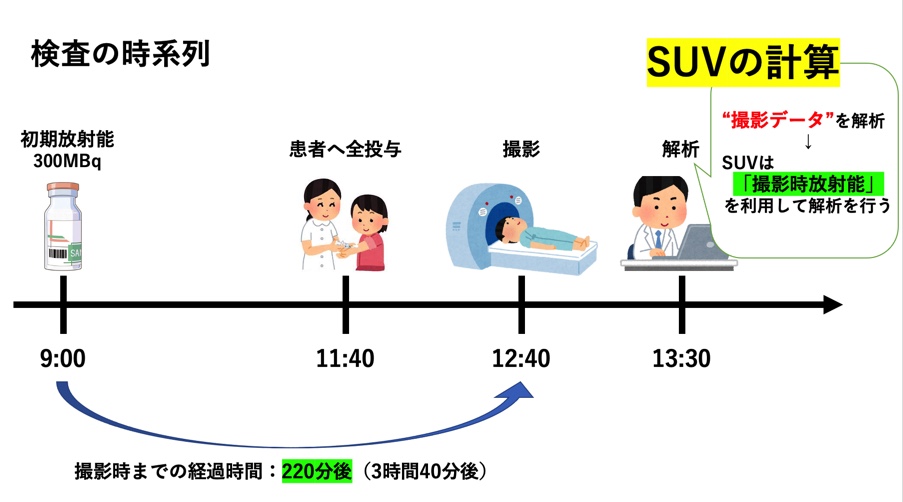
では図を使って時系列をまとめておきましょう

上図からも見てわかるようにSUVの計算は

『撮影時の放射能』

を利用することがわかります

用意されたFDGの初期値は300MBqで、撮影時には220分経過していることがわかります

FDGの半減期は110分であるので撮影時放射能は

$$300×\left(\frac{1}{2}\right)^2=75MBq$$

ここまで理解すればあとは計算は簡単ですね

$$SUV=\frac{目的組織の放射能濃度}{\frac{投与放射能量}{体重}}$$

本文より人体の比重1kg/Lで調整すれば

$$SUV=\frac{7.5×10^3[Bq/mL]}{\frac{75×10^6[Bq]}{60[kg]}×10^{-3}[kg/mL]}$$

これを計算するとSUV=６になり選択肢は『４』になります

お疲れ様でした